ARRAYS
- Introducción a los arrays
- Vectores
- Matrices
- Poliedros
- Ahorrar espacios en arrays de cadenas
- Matrices orladas
- Formaciones dinámicas
INTRODUCCIÓN A LOS ARRAYS
Hasta ahora hemos usado variables para guardar la información que maneja el programa. Una variable con su nombre y su tipo para cada dato (nombre, cantidad, nivel, precio, edad...) que nos hacía falta. Pero ¿Que ocurre si nuestro programa tiene que manejar una colección de datos muy grande como los nombres de una agenda o los precios de un catálogo? Se podría hacer usando 100 variables distintas pero el algoritmo llegaría a ser terriblemente complicado y muy poco funcional. En este apartado vamos a ver cómo podemos asignar un mismo nombre de variable para muchos datos y referirnos a cada uno de ellos de forma individual usando un número al que llamaremos índice.
Usaremos unas estructuras de datos llamadas Arrays, de las que se dice que son "Estructuras estáticas de almacenamiento interno".
- Son estáticas porque su tamaño se declara al principio del programa y ya no se puede modificar. Si hacemos un programa que trabaje con 100 nombres siempre lo hará con 100 aunque solo lleguemos a usar 20, y nunca podrá trabajar con más de 100.
- Son de almacenamiento interno porque están en la memoria RAM del ordenador, como variables que son, y su tiempo de vida sólo dura mientras se ejecuta el programa. Al terminar se pierde su contenido.
En programación normalmente se conocen como "Arrays" aunque su nombre más correcto en castellano sería "formaciones".
Como veremos en los apartados siguientes, los arrays de 1 dimensión se llaman vectores, los de 2 dimensiones se llaman matrices y los de 3 o más se llaman poliedros o arrays multidimensionales.
En informática muchas veces se llama vector a cualquier array. En la ayuda de QBasic (y de Visual Basic) siempre llaman Matriz a cualquier array, por lo que hay que tener cuidado de no liarse.
VECTORES
Imaginemos este bloque de pisos de cuatro plantas.

Vamos a escribir un programa de la forma que sabemos hasta ahora que nos pregunte el nombre de la persona vive en cada piso y una vez que ha recopilado toda esa información, nos deje preguntarle quien vive en el piso que nosotros queramos.
CLS
INPUT "Nombre de quien vive en el 1º: ", nombre1$
INPUT "Nombre de quien vive en el 2º: ", nombre2$
INPUT "Nombre de quien vive en el 3º: ", nombre3$
INPUT "Nombre de quien vive en el 4º: ", nombre4$
DO
INPUT "Escribe un piso para ver quien vive en él: ",n
LOOP WHILE (n < 1) OR (n > 4)
SELECT CASE n
CASE 1: PRINT "En el 1º vive "; nombre1$
CASE 2: PRINT "En el 2º vive "; nombre2$
CASE 3: PRINT "En el 3º vive "; nombre3$
CASE 4: PRINT "En el 4º vive "; nombre4$
END SELECT
El resultado podría ser este:
Nombre de quien vive en el 1º: Paca
Nombre de quien vive en el 2º: Manolo
Nombre de quien vive en el 3º: Lola
Nombre de quien vive en el 4º: Pepe
Escribe un piso para ver quien vive en él: 3
En el 3º vive Lola
Un listado un poco largo para hacer algo tan sencillo. Si en vez de cuatro pisos fueran 40 tendríamos un programa casi diez veces más largo con muchas partes casi iguales, pero que no podemos meter en bucles repetitivos porque cada variable es distinta. Observa que comprobamos que el piso sea entre 1 y 4, a partir de ahora va a ser muy importante depurar los datos de entrada, ya veremos por qué.
Ahora vamos a escribir un programa que haga lo mismo que el anterior, pero usando un VECTOR.
DIM nombre$ (1 TO 4)
FOR n = 1 TO 4
PRINT "Nombre de quien vive en el"; n; "º: ";
INPUT "", nombre$(n)
NEXT
DO
INPUT "Escribe un piso para ver quien vive: ",n
LOOP WHILE (n < 1) OR (n > 4)
PRINT "En el";n;"º vive ";nombre$(n)
El resultado sería similar, pero el listado es mucho más corto, especialmente todo el SELECT CASE anterior que se ha transformado en una sola instrucción.
Vamos a ver este programa línea a línea.
La primera instrucción es nueva. En ella lo que hacemos es DECLARAR una variable que se va a llamar nombre$ (como lleva el $ va a ser de tipo texto) y va a poder guardar cuatro valores a los que accederemos con subíndices que van desde el 1 hasta el 4. Para determinar este intervalo de valores hay que usar números enteros constantes, no valen expresiones matemáticas.
En el siguiente bloque FOR, que se ejecutará 4 veces lo que hacemos es ir pidiendo al usuario que escriba los nombres. La primera vez guardamos lo que escriba en la posición 1 del vector porque hacemos referencia al índice 1 entre paréntesis a continuación del nombre del vector. La siguiente vez al índice 2, la siguiente vez al 3 y la última vez que se ejecute el bucle hacemos referencia al índice 4. A esto es a lo que se llama "Recorrer el vector" ya que hemos hecho algo con cada uno de sus elementos. Normalmente esto lo haremos siempre con un bucle FOR, que es lo más cómodo.
La pregunta de "nombre de quien vive en..." no está en el INPUT porque esta instrucción no evalúa expresiones, por eso está antes en un PRINT normal con un punto y coma al final para que el cursor no pase a la siguiente línea.
Ahora ya tenemos dentro del vector los cuatro nombres para usarlos como queramos haciendo referencia al nombre del vector y al subíndice entre paréntesis. Para hacer referencia a los subíndices de un array se puede usar cualquier expresión, no tiene porqué ser un número constante, pero hay que tener cuidado de no hacer nunca referencia a índices que no existan
En el siguiente bloque pedimos al usuario que escriba el número de un piso y lo guardamos en la variable N. Obligamos a que sea un número entre 1 y 4.
Al final viene lo espectacular. Para acceder a cualquiera de los índices del vector se puede hacer directamente tomando el valor de la variable N como subíndice sin necesidad de controlar cada valor por separado como antes.
Vamos con otro ejemplo para que todo esto vaya quedando cada vez más claro.
En temas anteriores teníamos un programa para escribir el nombre de un mes a partir de su número. Lo hicimos con muchos IF anidados, después con ELSEIF y por último con SELECT CASE que ya quedaba mucho más corto, pero de ninguna forma nos libramos de escribir todo el SELECT CASE y todos los meses en cualquier parte del programa dónde queramos que se escriba el nombre de algún mes.
Ahora vamos a plantear el problema de otra forma:
DIM mese$ (1 TO 12)
mese$(1)="Enero"
mese$(2)="Febrero"
mese$(3)="Marzo"
mese$(4)="Abril"
mese$(5)="Mayo"
mese$(6)="Junio"
mese$(7)="Julio"
mese$(8)="Agosto"
mese$(9)="Septiembre"
mese$(10)="Octubre"
mese$(11)="Noviembre"
mese$(12)="Diciembre"
'(...)
PRINT mese$(2) 'Escribe Febrero
'(...)
n=6
PRINT mese$(n) 'Escribe Junio
Hemos declarado un vector de cadenas de 12 posiciones llamado mese$.
Al principio del programa llenamos el vector con los nombres de los meses, cada uno en su lugar correcto.
Donde nos haga falta el nombre de un mes sólo tendremos que usar el vector y referirnos al mes que queramos. De esta forma meses(3) nos devolverá "Marzo" y si n vale 11 entonces meses(n) nos devolverá "Noviembre".
En los dos ejemplos que hemos puesto los índices de los vectores han empezado en el 1, pero esto no tiene que ser siempre así. En QBasic pueden empezar por cualquier número incluso negativo, aunque lo más normal es que siempre empiecen por 1 o por 0. El valor más bajo posible para los índices es -32768 y el más alto es 32767. Por supuesto el final del intervalo no puede ser menor que el principio. Veamos algunos ejemplos más de declaración de vectores.
DIM alumno$(1 TO 30) '30 cadenas
DIM nota (1 TO 30) '30 números reales
DIM ventas_verano%(6 TO 9) '4 enteros
También podemos declarar vectores de un solo elemento, aunque esto puede que no tenga mucho sentido.
DIM número (1 TO 1)
Para determinar el tamaño de cualquier vector usamos la siguiente fórmula:
ÚLTIMO INDICE - PRIMER ÍNDICE + 1
Así en el ejemplo de los meses resulta 12 - 1 + 1 = 12 elementos, muy sencillo ¿no? pero a veces terminaremos contando con los dedos.
Para inicializar un vector (Borrarlo entero) no hace falta recorrerlo, podemos hacer:
ERASE (nombre_vector)
Y el vector se quedará lleno de ceros si es numérico o de cadenas vacías ("") si es de cadenas.
Recordemos que en QBasic todas las variables están a cero al principio, pero en otros lenguajes no.
Ahora vamos a ver el problema más típico de los vectores (y en general de todos los arrays).
No podemos intentar acceder a subíndices que no existen. En caso de que llegue a ocurrir en QBasic se producirá un error de tipo "Subíndice fuera del intervalo" y el programa se detendrá sin mayores consecuencias.
En muchos otros lenguajes no ocurrirá nada, pero si estamos leyendo sacaremos datos de otras posiciones de memoria que no son nuestras de más allá del final del vector y si estamos escribiendo lo haremos sobreescribiendo otros datos importantes para el programa o incluso para el sistema operativo (DOS o WINDOWS) con lo que casi seguro conseguiremos que el ordenador se quede bloqueado.
Imagina que en un programa (No de QBasic) ocurre esto y va a parar a un registro estratégico del sistema operativo un número que equivale de alguna forma a la llamada al programa de formatear el disco duro, no veas el estropicio.
De ahí la importancia de depurar los datos de entrada, especialmente los que van a servir como índices para arrays. Si en nuestro primer ejemplo no depuramos el dato del piso que pedimos al usuario y este escribe uno que no está entre cero y cuatro, al acceder al vector se produciría este error.
MATRICES
Ahora imaginemos este otro bloque de pisos, para el que tenemos que hacer un programa similar al anterior.
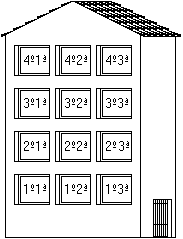
Vamos a escribir el programa. Será igual que el anterior, habrá que controlar las cuatro plantas pero además dentro de cada una habrá que controlar las tres puertas que hay en cada rellano (1ª, 2ª y 3ª).
DIM nombre$ (1 TO 4, 1 TO 3)
FOR piso = 1 TO 4
FOR puerta = 1 TO 3
PRINT "Nombre de quien vive en el"; piso; "º"; puerta; "ª: ";
INPUT "", nombre$(piso, puerta)
next
NEXT
PRINT "Para saber quien vive en un piso..."
DO
INPUT " Escribe el piso: ",piso
LOOP WHILE (piso < 1) OR (piso > 4)
DO
INPUT " Escribe la puerta: ",puerta
LOOP WHILE (puerta < 1) OR (puerta > 3)
PRINT "En el";piso;"º";puerta;"ª vive ";nombre$(piso, puerta)
Se puede ver que es muy parecido, pero hemos utilizado una MATRIZ, que es un array de dos dimensiones, mientras que un vector es un array de una sola dimensión. Por si hay alguna duda de lo que hace este programa vamos a ver un posible resultado.
Nombre de quien vive en el 1º 1ª: Paca
Nombre de quien vive en el 1º 2ª: Gloria
Nombre de quien vive en el 1º 3ª: Fernando
Nombre de quien vive en el 2º 1ª: Mari
Nombre de quien vive en el 2º 2ª: Juan
Nombre de quien vive en el 2º 3ª: Manolo
Nombre de quien vive en el 3º 1ª: Lola
Nombre de quien vive en el 3º 2ª: Rosa
Nombre de quien vive en el 3º 3ª: Mario
Nombre de quien vive en el 4º 1ª: Pepe
Nombre de quien vive en el 4º 2ª: Nacho
Nombre de quien vive en el 4º 3ª: Luisa
Para ver quien vive en un piso...
Escribe la planta: 3
Escribe la puerta: 2
En el 3º 2ª vive Rosa
Lo más novedoso es la forma de declarar la matriz, igual que el vector pero esta vez habrá que usar dos intervalos separados por una coma. Y por lo tanto siempre que nos refiramos a la matriz habrá que usar dos subíndices.
Para recorrer la matriz hay que usar dos FOR anidados. Esta vez la hemos recorrido por filas (pisos en nuestro ejemplo) ya que el "FOR piso" está fuera y hasta que no se ejecute entero el "FOR puerta" en cada piso no pasamos al siguiente. Para recorrerla por columnas (puertas) bastaría con intercambiar los FOR:
FOR puerta = 1 TO 3
FOR piso = 1 TO 4
'(...)
next
NEXT
Para el ordenador es completamente intrascendente que lo hagamos de una forma u otra, él no entiende de filas horizontales ni columnas verticales, de hecho almacena todos los elementos seguidos uno detrás de otro y hace operaciones matemáticas con los dos subíndices para determinar la única posición del elemento.
Esto se puede ver fácilmente pensando en la posición de los buzones de correos en el portal del bloque de pisos.
![]()
Cada piso tiene su buzón, el del 2º 2ª es el quinto porque tiene delante los tres de la primera planta y es el segundo de la segunda. Para calcular las posiciones se hace algo así como ((PLANTA-1)*Nº_total_de_PUERTAS)+PUERTA, que sale ((2-1)*3)+2 = 5.
A nosotros esto no nos interesa porque lo hace QBasic automáticamente. Si programamos en otros lenguajes más primitivos sí que habría que preocuparse de esto porque sólo existen vectores de una dimensión.
1.12.4 - POLIEDROS
Lo más normal es usar vectores (1 dimensión) o matrices (2 dimensiones), pero QBasic puede llegar a manejar arrays con hasta 60 dimensiones!!!
Veamos un caso rebuscado de un array de tres dimensiones ampliando los ejemplos anteriores de los bloques de pisos.
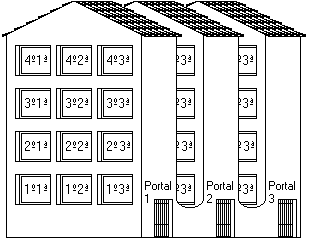
En este caso nuestro bloque tiene tres portales (1 a 3) y cada uno de ellos tiene cuatro plantas y tres puertas igual que antes.
Para declarar el poliedro habría que hacer:
DIM nombre$ (1 TO 3, 1 TO 4, 1 TO 3)
La primera dimensión va a ser para los portales, la segunda para los pisos y la tercera para las puertas.
Para recorrer el array haríamos:
FOR portal = 1 TO 3
FOR piso = 1 TO 4
FOR puerta = 1 TO 3
'(...)
NEXT
NEXT
NEXT
Esta vez tenemos tres bucles FOR anidados y las instrucciones que pongamos dentro de todo se ejecutarán 36 veces que es el producto de todas las dimensiones.
Ya empezamos a liarnos pensando en recorrer el array primero por portales o no, etc... Todavía podemos tener una representación visual del problema, pero si usamos arrays de cuatro, cinco o más dimensiones ya esto no será así y la habremos liado del todo. En estos casos lo mejor será plantear el problema de otra forma o usar estructuras de datos más flexibles que ya veremos más adelante.
AHORRAR ESPACIO
EN LOS ARRAYS DE CADENAS
Hasta ahora no hemos sido demasiado estrictos en el ahorro de memoria ya que ni siquiera estamos declarando las variables. Nuestros programas de QBasic son muy sencillos y usan muy pocas variables, pero al trabajar con arrays hay que darse cuenta que basta con declarar una matriz de 20 por 20 elementos para que se gasten 400 posiciones de memoria.
En las cadenas QBasic no nos limita el número de caracteres que vamos a poder meter en ellas y para que esto funcione se gasta cierta cantidad de memoria (unos 10 bytes), que si multiplicamos por 400 posiciones de memoria son casi 4 KB, una cantidad respetable para programas tan pequeños.
Puede ocurrir que en nuestra matriz de cadenas no lleguemos a almacenar palabras más largas de por ejemplo 15 letras con los que nos convendría limitar el tamaño de las cadenas y ahorrarnos esos 10 bytes en cada posición.
Para declarar un array de cadenas de tamaño limitado haríamos:
DIM matriz(1 TO 20, 1 TO 20) AS STRING * 15
Las palabras clave AS STRING declaran explícitamente la variable como de tipo cadena (Esta será la forma normal de hacerlo en Visual Basic), por eso ya no es necesario poner el $ al final del nombre. Si a continuación ponemos un asterisco y un número estamos limitando el tamaño de las cadenas con lo que QBasic ya no tendrá que determinarlo automáticamente constantemente, con lo que ahorraremos memoria y el programa funcionará algo más rápido.
Si asignamos a estas variables una cadena de más de 15 caracteres no ocurre nada, simplemente la cadena se corta y sólo se almacenan los primeros 15 caracteres, los demás se pierden.
En los tipos numéricos no podemos ahorrar nada, pero en los arrays de cadenas deberíamos hacer siempre esto, especialmente si van a contener muchos elementos.
MATRICES ORLADAS
Imaginemos el juego del buscaminas en el que tenemos una matriz de 8 por 8 elementos (Casillas) que van a contener un 1 si contienen una mina o un cero si están vacías.
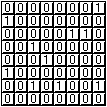
Cuando el usuario destape una casilla, si no contiene una mina, habrá que escribir el número de minas que la rodean. Para hacer esto habrá que sumar los valores de las casillas que hay arriba a la izquierda, arriba, arriba a la derecha, a la derecha, abajo a la derecha, abajo, abajo a la izquierda y a la izquierda.
Si estamos en una casilla del interior del tablero esto funciona perfectamente, pero si estamos en el borde nos encontramos con el problema de que haríamos referencia a posiciones de fuera de la matriz con lo que se produciría un error de "Subíndice fuera del intervalo".
Para evitar esto habría que comprobar que si estamos en el borde superior no se cuenten las casillas superiores, si estamos en el inferior no se cuenten las de abajo, si estamos en una esquina solo se cuenten las tres de dentro, etc. con lo que tendríamos en total nueve rutinas diferentes, así como que controlar cual de ellas usar según por donde esté la casilla que estamos destapando.
Para solucionar este problema lo que se suele hacer es dotar a la matriz de más filas y columnas de forma que todos los elementos que realmente nos interesan estén rodeados por un "borde" de elementos vacíos que estarán ahí sólo para poder hacer referencia a ellos sin salirnos de la matriz.
Una representación gráfica de la matriz orlada podría ser esta, donde hay un borde de "casillas" que no vamos a usar nunca para poner minas, pero a las que podemos referirnos siempre que sea necesario sin salirnos de la matriz. En el ejemplo que nos ocupa, estas posiciones contendrían el valor 0 ya que están vacías.

Esta técnica se aplica mucho en juegos de este tipo, en programas de imágenes y en cualquier lugar donde se tenga que acceder a posiciones de una matriz y puedan producirse problemas en los bordes. En el caso de vectores habría que añadir un elemento más al principio y otro al final, para los poliedros sería como envolverlo completamente y en el caso de arrays de más de cuatro dimensiones ya es difícil imaginarse como se haría.
Hay que recordar que en QBasic se pueden usar subíndices negativos, pero en la mayoría de otros lenguajes de programación esto no es así.
El único inconveniente de las matrices orladas es que ocupan más memoria, exáctamente (2*(alto+ancho))+4 posiciones más. Este gasto de recursos está justificado en la mayoría de los casos ya que se consigue simplificar mucho los programas.
FORMACIONES DINÁMICAS
En otros lenguajes de programación más avanzados como C o Pascal existen lo que se llaman "Estructuras de almacenamiento dinámicas" que son técnicas de programación que mediante la utilización de punteros (Variables especiales que contienen direcciones de memoria) permiten acceder directamente a la memoria del ordenador y colocar los datos en estructuras como listas enlazadas, árboles, pilas, colas, tablas hash, etc cuyo tamaño cambia constantemente durante la ejecución del programa sin estar definido de ninguna forma en el código del programa. Por eso se dice que son estructuras de almacenamiento dinámicas.
Como QBasic (ni Visual Basic) no trabaja directamente con punteros no podemos llegar a utilizar estas estructuras. En algún caso puede suceder que necesitemos almacenar elementos en un array (Vector, matriz, etc...), pero no podamos saber de antemano cuanto grande va a tener que ser y tampoco nos merezca la pena poner un límite arbitrario que se alcanzará en seguida o bien no llegará a ser usado nunca desperdiciando mucha memoria.
Para solucionar en parte este problema QBasic nos da la posibilidad de declarar los arrays usando la instrucción REDIM en lugar de DIM y después en cualquier parte del programa poder redimensionarlos tantas veces como queramos usando valores que pueden ser variables.
Veamos un ejemplo:
REDIM mat(1 TO 1)
INPUT "¿Cuantos números vamos a almacenar?", maxi
REDIM mat(1 TO maxi)
FOR n = 1 TO maxi
INPUT mat(n)
NEXT
INPUT "¿Cuantos números vamos a almacenar ahora?", maxi2
REDIM mat(1 TO maxi2)
FOR n = 1 TO maxi2
INPUT mat(n)
NEXT
Se puede ver que declaramos un vector de enteros de sólo un elemento usando REDIM, a continuación pedimos al usuario que escriba un número y después volvemos a redimensionar el vector con este número de elementos para ya recorrerla como hemos hecho siempre. A continuación repetimos el proceso volviendo a redimensionar el vector, perdíendose la primera serie de números que almacenó en ella el usuario.
Aquí hay que aclarar algunas cosas:
- La primera orden REDIM mat(1 to 1) nos la podíamos haber ahorrado, pero siempre es costumbre declarar las variables al principio del programa para tener una visión global de las variables que hay sin tener que recorrer el listado completo.
- Si al declarar un array con la orden DIM usamos variables en vez de valores constantes lo declaramos como dinámico y después podrá ser redimensionado.
- Para redimensionar un array dinámico ya existente habrá que hacerlo siempre con la orden REDIM y en QBasic tendremos que usar las dimensiones que ya tiene, es decir, si antes era una matriz con dos dimensiones al redimensionarlo tenemos que especificar dos intervalos, ni más ni menos, y por supuesto el mismo tipo de datos.
- Al redimensionar un array se borran todos los valores que tuviera, quedando entero inicializado a valores cero o cadenas vacías.
Visto esto sólo queda por decir que siempre que sea posible se evite el uso de arrays dinámicos ya que el manejo interno de la memoria es mucho menos eficiente y podría dar lugar a errores como los típicos de "Memoria agotada". Para evitar que los arrays sean dinámicos usar siempre valores constantes (números) para definir sus dimensiones al declararlos con la orden DIM al principio del programa.